Algoritmo del PageRank
Texto extraido de www.thesmokesellers.com bajo licencia de Creative Commons.
Method for node ranking in a linked database
![]()
(Método para la jerarquización de nodos en una base de datos enlazada)
La patente más famosa de Google es una de las principales ventajas competitivas que permitió a esta compañía aplastar a sus competidores en el campo de las busquedas en internet y hacerse el gigante que son hoy*. El Page Rank, como todos la conocemos, es una idea genial para hallar el valor o "importancia" que tiene una página web determinada. Esta "importancia" se emplea después para mostrar los resultados de mayor calidad cuando realizamos una búsqueda en Google. La calidad de los resultados de Google empleando este método (combinado, por supuesto, con otros algoritmos) es lo que nos hizo a todos abandonar nuestros antiguos buscadores (Altavista, Metacrawler) y pasarnos al buscador de Larry y Sergei. En este post vamos a explicar el algoritmo hasta el final intentando emplear la cantidad mínima de matemáticas posibles.
Si alguna vez te has interesado por el tema, habrás leido que:
1. La "importancia" de una página web sólo depende de las paginas web que la enlazan.
Si tienes una página web y esta es enlazada desde páginas importantes (de alto Page Rank, pongamos (www.microsiervos.com) tú recibiras una parte de esa importancia. Todas las páginas que enlaces desde tu página web (ese blog de tu colega con solo dos posts, por ejemplo) recibirán, a su vez, una parte de la importancia de TU página. Para ser más exactos:
2. Una página web reparte por igual su importancia entre todas las páginas a las que enlaza.
Es decir: Si te enlaza una página importante que enlaza 3 o 4 páginas a parte de la tuya es mucho mejor que si te enlaza una página igual de importante que enlace 30 o 40 (toca más Page Rank a repartir).
También habrás oído hablar de los Spiders (arañas). Esto no son más que veloces programas automáticos que van recorriendo internet como si fuesen un usuario humano, pulsando todos los enlaces posibles, extendiendose así por la "red" (de ahí el nombre) y creando un mapa de la misma. Así que tenemos:
3. Los Spiders proporcionan a Google un mapa de la red donde se puede ver qué página apunta a que página
Esto no significa que sepamos ya el Page Rank. De hecho, todo esto es muy bonito pero… como leches calculamos el Page Rank?. Por qué página empezamos?. Suponiendo que empezásemos por una, si no tenemos el Page Rank de las que enlazan a esta, como podemos calcular algo?. Y lo que es peor: En internet hay venticincomil millones de páginas apuntandose unas a otras (número subiendo rápidamente), cómo crear un algoritmo que sea capaz de lidiar con semejante brutalidad de enlaces. En el peor caso todas las páginas se apuntan entre si y el numero total de enlaces es de venticincomil millones, al cuadrado!!.
Aquí es donde realmente llega la artillería matemática. Prometemos que si sabes lo que es una matriz, como se suman y como se multiplican (y tienes un poco de fe) ya puedes entender el algoritmo de Larry y Sergei hasta el final.
La Matriz de reparto de Page Rank H
Vale, no sabemos cual es el page Rank de ninguna página antes de empezar, pero si hay una cosa que sabemos: Cuanto de su desconocido Page Rank reparte una página entre las páginas que enlaza. Por lo dicho en (2), si una página enlaza 5 páginas transmitirá un 1/5 de su Page Rank a cada una. Debido a (3) el número de páginas que enlaza cada página lo sabemos. Es más, podemos construir una tabla H de veinticinco mil millones de filas por veinticinco mil millones columnas (no, no cabe en un A4), que contenga todos los enlaces posibles. Para dos páginas cualesquiera (una como enlazadora y la otra como enlazada) tenemos un recuadro de la tabla que nos indica que proporción del Page Rank transfiere la enlazadora a la enlazada. Para orientarnos un poco: La diagonal de esta tabla representaría lo que la página se transmite a si misma (si se enlazase). Cualquier recuadro por debajo de la diagonal y su simétrico por encima de la diagonal indican respectivamente lo que se transmiten dos páginas cuando una actúa como enlazadora y la otra como enlazada y viceversa. Si una página no enlaza a otra, se pone un 0 en el recuadro (lógicamente no le puede transmitir nada de Page Rank).
Matriz (Vector) Invariante I
Lo que viene a continuación no es idea de Larry Page o Sergei Brin, hace un siglo que se conoce, pero si que requiere la poca de fe que te pedimos reservar. Esta tabla (lease Matriz), que hemos creado con la ayuda de la información proporcionada por los Spiders, representa en realidad la dificultad (o facilidad) para el "flujo" de Page Rank de una página a otra. Podemos ver el flujo como agua que pasa con menor o mayor dificultad de una página a otra de acuerdo al valor correspondiente al recuadro de la tabla H. Este agua/transferencia de Page Rank fluiría de una página a otra a través de sus enlaces sin cesar y eventualmente podría llegar a un equilibrio (si no llegase no habría Page Rank alguno). Pues bien las matemáticas, concretamente el teorema de Ruelle-Perron–Frobenius (ingles) nos garantiza lo siguiente:
4. Bajo determinadas condiciones, que veremos, se acabará alcanzando ese equilibrio. No es que Frobenius (ingles) supiese lo que es una página web en 1900, si no que el problema es matemáticamente idéntico a un conocido problema de dinámica de sistemas (ingles). Luego, hay gente que dice que Larry y Sergei son licenciados en filosofía.
5. El equilibrio queda representado por el vector invariante I. Esto es: Una tabla de una sola columna (una matriz, más concretamente vector) de venticincomil millones de valores, que cumple que al multiplicarla por la matriz de reparto H nos da otra vez ella misma (I). Lo que expresaríamos:
![]()
Este vector invariante I de venticincomil millones de valores, que casualidad, uno para cada página web, es el Page Rank. Faltará refinarlo, escalandolo de 1 a 10, y discretizarlo para que no de valores intermedios. Intuyo que el valor discretizado (1 a 10 sin decimales), que se muestra en la google toolbar, es solo de cara al publico e internamente emplearan los decimales que salgan también.
Sí, muy guay pero y lo de las 25.000.000.000 páginas?
Cierto, cierto. La gente que haya sufrido álgebra de primero habrá reconocido a I como un vector propio de valor propio 1 de la matriz H. Y seguramente recordará con horror que para calcularlo hay que resolver un polinomio que en este caso tendría grado 25.000.000.000. Vamos no lo calculamos así ni de blas. Afortunadamente, sobre todo para las personas a las que lo anterior les ha sonado a chino, existe un método para calcular I iterativamente (en pasos sucesivos) y muy muy sencillo. Tan sencillo que consiste en que nos inventamos una tabla de 25.000.000.000 valores del Page Rank a voleo (un vector I0 creado aleatoriamente), lo multiplicamos por H y el resultado será otra tabla de 25.000.000.000 valores I1 pero más cercanos al valor correcto del vector invariante I. Repítase esto un montón de veces hasta que el resultado de multiplicar por H ya no produzca ningún cambio y ya está. Ya tenemos el vector invariante. Este algoritmo, que se llama el método de las potencias (ingles), se expresaría matemáticamente así:
![]()
Donde k no es más de que el índice que indica cuantas veces hemos multiplicado por la matriz H. El primer vector, que creariamos a boleo sería k = 0, el segundo, procedente de multiplicar por H sería k =1, etc. Para expresar de forma general que cada término se obtiene mediante una transformación del anterior se emplean los índices k+1 y k. Hay que tener en cuenta que los métodos iterativos tienen la ventaja de que no necesitamos acumular demasiados valores, lo cual reduce la cantidad de memoria que necesitamos para computar el Page Rank y acelera todo el proceso de cálculo. Siguen siendo una burrada de números pero al menos es factible.
Gran problema
Que fácil, no?. Obviamente falla algo y ese algo es el punto (4). Resulta que no se cumplen las condiciones de convergencia del teorema Ruelle-Perron–Frobenius. Es decir que aplicando el método arriba explicado no hay garantía de que lleguemos al vector invariante. No entraré en detalles, no hace falta. Utilizando la analogía del "flujo" de Page Rank se puede entender perfectamente que es lo que falla y como se puede solucionar.
Página Sumidero:
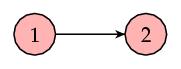 Qué ocurre cuando el flujo de Page Rank llega a una página como la 2 que no tiene enlaces a ningún sitio?. Pues simplemente que no sale de ahí. Esa página se vuelve un sumidero de Page Rank y el algoritmo dará resultados incorrectos. Como lo resolvemos?. Si hacemos la página 2 enlace todas las páginas de la web por igual (imagina millones de pequeñas flechas saliendo de 2 hacia todas lás páginas), esto dará salida al flujo de Page Rank pero la influencia en los resultados es mínima, puesto que cada página recibe solo 1/25.000.000.000 del Page Rank de 2. Matemáticamente, esto equivale a sumarle a H una matriz A que tenga todo 0s menos en las columnas de las páginas sumidero que tendrán toda la columna llena de 1/25.000.000.000. De esta forma en vez de la matriz H emplearíamos la matriz S=H+A en el método de las potencias.
Qué ocurre cuando el flujo de Page Rank llega a una página como la 2 que no tiene enlaces a ningún sitio?. Pues simplemente que no sale de ahí. Esa página se vuelve un sumidero de Page Rank y el algoritmo dará resultados incorrectos. Como lo resolvemos?. Si hacemos la página 2 enlace todas las páginas de la web por igual (imagina millones de pequeñas flechas saliendo de 2 hacia todas lás páginas), esto dará salida al flujo de Page Rank pero la influencia en los resultados es mínima, puesto que cada página recibe solo 1/25.000.000.000 del Page Rank de 2. Matemáticamente, esto equivale a sumarle a H una matriz A que tenga todo 0s menos en las columnas de las páginas sumidero que tendrán toda la columna llena de 1/25.000.000.000. De esta forma en vez de la matriz H emplearíamos la matriz S=H+A en el método de las potencias.
Red-Sumidero:
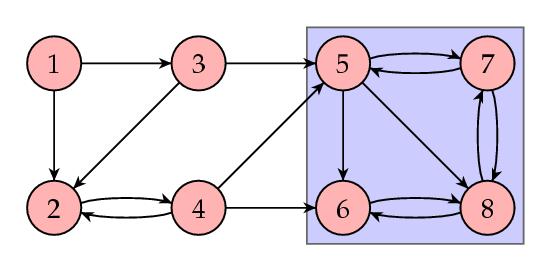
Un caso similar es el de las sub-redes de páginas dentro de la red, como la 5-7-6-8, que no tienen enlaces de vuelta. Estas redes se convierten en redes-sumidero. El problema es que estas páginas sí enlazan otras páginas y no podemos simplemente cargarnos esa información y enlazar todas las páginas de la red desde ellas. Para dar salida al flujo de Page Rank, vamos a recurrir a una solución al más puro estilo "ingeniero".
Gran solución
Necesitamos garantizar la salida del flujo de Page Rank de cualquier página o sub-red, es decir, que toda página apunte a otra página. No nos vale con crear un enlace a cualquier página a boleo porque (a parte de estar falseando el Page Rank), si resulta en una red cerrada como 5-7-6-8 no hemos solucionado nada. Ahora, imaginemos un caso ideal en donde todas las páginas apuntasen a todas las páginas. Ahí el Page Rank siempre tendría algún enlace por donde escapar, incluso de las sub-redes, y el algoritmo funcionaría. Pero claro, se perdería toda la jerarquía que dan los enlaces, la matriz de reparto tendría todos sus elementos iguales a 1/25.000.000.000 y todas las páginas tendrían el mismo Page Rank.
Pues nada, sumo la matriz de reparto real, calculada con la información de los Spiders con la ideal en la que todas las páginas se apuntan entre si y lo divido por dos. La matriz resultante tendrá siempre enlaces saliedo de cada página y tenemos el flujo de Page Rank garantizado. Que al mezclar a partes iguales la matriz real y la ideal me salen los resultados demasiado aleatorios? (por influencia de la ideal). Bueno, pues en vez de mitad y mitad las mezclo con 85% de la matriz real y un 15% de la ideal y pista. Y ya esta señores. Con ustedes la famosa matriz de Google:
![]()
Donde recordemos que S=H+A es la matriz real con el problema de los sumideros individuales resuelto, 1/n×1, con n = 25.000.000.000 es la matriz ideal y α = 0.85 nos da la citada mezcla al 85%. Algún lector avispado puede decir: Pero… el meter ahi un 15% de aleatoriedad, no falsea de alguna manera el Page Rank?… Bienvenido al mundo de la ingeniería chaval!.
Para terminar si empleamos G en vez de H en el método de las potencias y jugamos un poco con los términos obtenemos la formula que aparecía al principio del post. Empleando la fórmula a la derecha del igual obtendremos cada nuevo vector Ik+1 en cada iteración.
![]()
Anotaciones finales
Este artículo esta confeccionado a partir de esta maravillosa página (ingles) (de la que también tomé "prestadas" las imágenes) y la imprescindible ayuda de la Wikipedia. En la página también hay enlaces a los pdf originales de Larry y Sergei así como a algún libro sobre el tema. Si alguien se toma la molestia de echarle un vistazo, ahí van algunas aclaraciones:
- El valor óptimo del parámetro α se determina experimentalemente y regula también la velocidad de convergencia del metodo de las potencias, a mayor porcentaje de matriz real, menor velocidad de convergencia. Google dice que con basta con k=50-100 iteraciones para calcular el Page Rank, cosa que tarda varios días. Imagino que trabajando con varios ordenadores en paralelo. Esto se conoce como Google Dance y en TSS no nos hace ni puta gracia.
- Matemáticamente, la condición de convergencia del algoritmo empleado por Google es que todos los elementos de la matriz de reparto de Page Rank sean estictamente mayores que 0, cosa que cumple la chapucilla que acabamos de ver. Esto no es una condición de convergencia del metodo de las potencias si no una condición para la existencia del vector invariante según el teorema de Ruelle-Perron–Frobenius.
¿Quieres un botón con tu PageRank GRATIS?
Pasa por nuestra sección de botones, elige el que mas te guste, lo pegas en tu web y tendrás tu PageRank cada vez que se cargue tu página.

